KNLanczosMethod.cpp File Reference

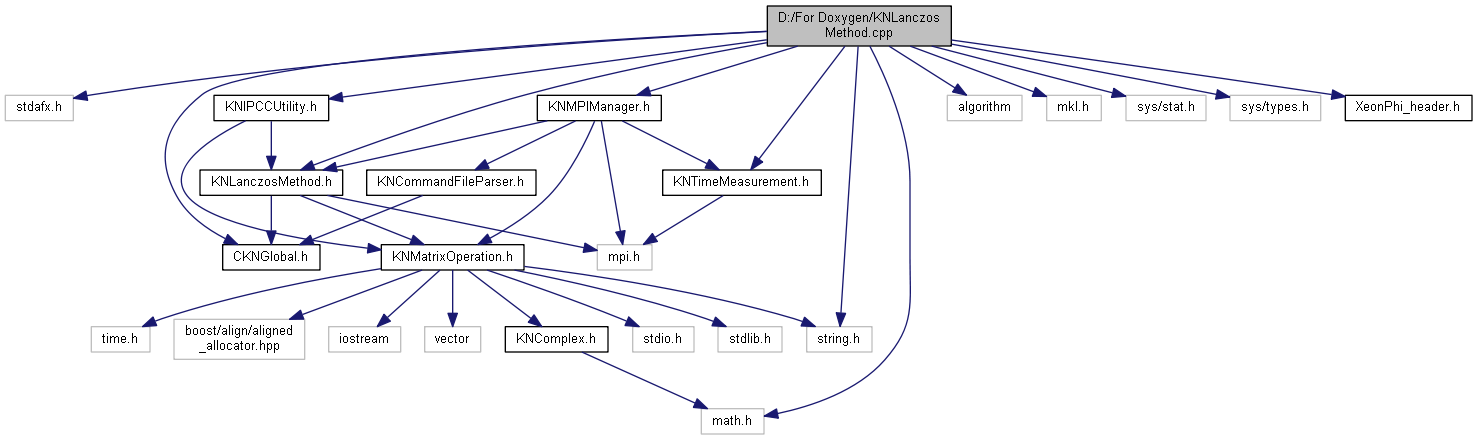
Lanczos method implementation class. More...

#include "stdafx.h"
#include "KNLanczosMethod.h"
#include "KNTimeMeasurement.h"
#include <math.h>
#include <string.h>
#include <algorithm>
#include "CKNGlobal.h"
#include "KNIPCCUtility.h"
#include "KNMPIManager.h"
#include "mkl.h"
#include <sys/stat.h>
#include <sys/types.h>
#include "XeonPhi_header.h"

Include dependency graph for KNLanczosMethod.cpp:

Go to the source code of this file.

Macros
#define	SET_RESULT_TO_PARAMETER(pResultValue, pResultVector, nResultCount)

Functions
void	thomas_alg (double **T, double *initguess, double *app_evc, int iter)
void	inverse_iter (double *alpha, double *beta, double *app_evc, int iter, double app_eva)

Variables
unsigned int	X_largest

Detailed Description

Lanczos method implementation class.

Date

27/May/2014

Author

Kyu Nam Cho(mysto.nosp@m.us@k.nosp@m.orea..nosp@m.ac.k.nosp@m.r), Hoon Ryu(elec1.nosp@m.020@.nosp@m.gmail.nosp@m..com)

Definition in file KNLanczosMethod.cpp.

Macro Definition Documentation

#define SET_RESULT_TO_PARAMETER	(		pResultValue,
			pResultVector,
			nResultCount
	)

Value:

pCalcuResult_Value = pResultValue;          \
    pCalcuResult_Vector = pResultVector;        \
    nCalculatedEigenValueCount = nResultCount

Definition at line 858 of file KNLanczosMethod.cpp.

Function Documentation

void inverse_iter	(	double *	alpha,
		double *	beta,
		double *	app_evc,
		int	iter,
		double	app_eva
	)

Definition at line 790 of file KNLanczosMethod.cpp.

References thomas_alg().

Referenced by CKNLanczosMethod::DoEigenValueSolving().

{   //[completed]
    int i, j, k, iteration = 20;
    double temp = 0, err, etol = 1e-13;

    double *initguess = (double *)malloc(sizeof(double)*iter); // Initial Guess
    double **T = (double **)malloc(sizeof(double)* 2);

    for (i = 0; i<2; i++)
        T[i] = (double *)malloc(sizeof(double)*iter);

    for (i = 0; i<iter; i++)
        initguess[i] = 1 / sqrt((double)iter);

    for (k = 0; k<iteration; k++)
    {
        for (i = 0; i<2; i++)
        {
            if (i == 1)
            {
                for (j = 0; j<iter; j++)
                    T[i][j] = alpha[j] - app_eva;

            }
            else
            {
                for (j = 0; j<iter; j++)
                    T[i][j] = beta[j];
            }
        }

        thomas_alg(T, initguess, app_evc, iter);   // Solve (T-app_eva*I)*app_evc=initguess

        temp = 0;
        for (i = 0; i<iter; i++)
            temp += app_evc[i] * app_evc[i];

        for (i = 0; i<iter; i++)
            app_evc[i] = app_evc[i] / sqrt(temp);

        temp = 0;
        for (i = 0; i<iter; i++)
        {
            if (i == 0)
                temp += app_evc[i] * (alpha[i] * app_evc[i] + beta[i] * app_evc[i + 1]);
            else if (i == iter - 1)
                temp += app_evc[i] * (beta[i - 1] * app_evc[i - 1] + alpha[i] * app_evc[i]);
            else
                temp += app_evc[i] * (beta[i - 1] * app_evc[i - 1] + alpha[i] * app_evc[i] + beta[i] * app_evc[i + 1]);
        }

        err = app_eva - temp;
        if (fabs(err) < etol)
            break;

        if (k<iteration - 1)
        {
            for (i = 0; i<iter; i++)
                initguess[i] = app_evc[i];
        }
    } // Iteration k

    for (i = 0; i<2; i++)
        free(T[i]);
    free(T);
    free(initguess);
}

Here is the call graph for this function:

Here is the caller graph for this function:

void thomas_alg	(	double **	T,
		double *	initguess,
		double *	app_evc,
		int	iter
	)

Definition at line 725 of file KNLanczosMethod.cpp.

Referenced by inverse_iter().

{ //[completed]

    int i;
    double temp, tbeta = T[0][0];

    double *P = (double *)malloc(sizeof(double)*iter);

    //Forward Elimination   
    for (i = 0; i<iter - 1; i++)
    {
        if (fabs(T[1][i])>fabs(tbeta))
        {
            initguess[i + 1] -= initguess[i] * tbeta / T[1][i];
            T[1][i + 1] -= T[0][i] * tbeta / T[1][i];
            P[i] = 0;
            tbeta = T[0][i + 1];
        }
        else
        {
            temp = initguess[i + 1];
            initguess[i + 1] = initguess[i];
            initguess[i] = temp;

            temp = T[1][i + 1];
            T[1][i + 1] = T[0][i];
            T[0][i] = temp;

            initguess[i + 1] -= initguess[i] * T[1][i] / tbeta;

            T[1][i + 1] -= T[0][i] * T[1][i] / tbeta;

            if (i != iter - 2)
            {
                P[i] = T[0][i + 1];
                T[0][i + 1] = -P[i] * T[1][i] / tbeta;
            }

            T[1][i] = tbeta;

            if (i != iter - 2)
                tbeta = P[i];
        }
    }

    //Backward Substitution
    for (i = iter - 1; i>-1; i--)
    {
        if (i == iter - 1)
            app_evc[i] = initguess[i] / T[1][i];
        else if (i == iter - 2)
        {
            app_evc[i] = initguess[i] - app_evc[i + 1] * T[0][i];
            app_evc[i] = app_evc[i] / T[1][i];
        }
        else
        {
            app_evc[i] = initguess[i] - app_evc[i + 1] * T[0][i] - app_evc[i + 2] * P[i];
            app_evc[i] = app_evc[i] / T[1][i];
        }
    }

    free(P);
}

Here is the caller graph for this function:

Variable Documentation

unsigned int X_largest

Definition at line 27 of file KNLanczosMethod.cpp.

Referenced by CKNMatrixOperation::MVMulEx_AsyncCommWithLocalBlocks().